Comprendre le cercle trigonométrique
* Article principalement utile aux élèves qui suivent les cours suivants
Mathématiques secondaire 5 (séquence CST, TS, SN), Calcul différentiel, ondes et physique moderne (sections MHS, ondes stationnaires et ondes progressives mécaniques)
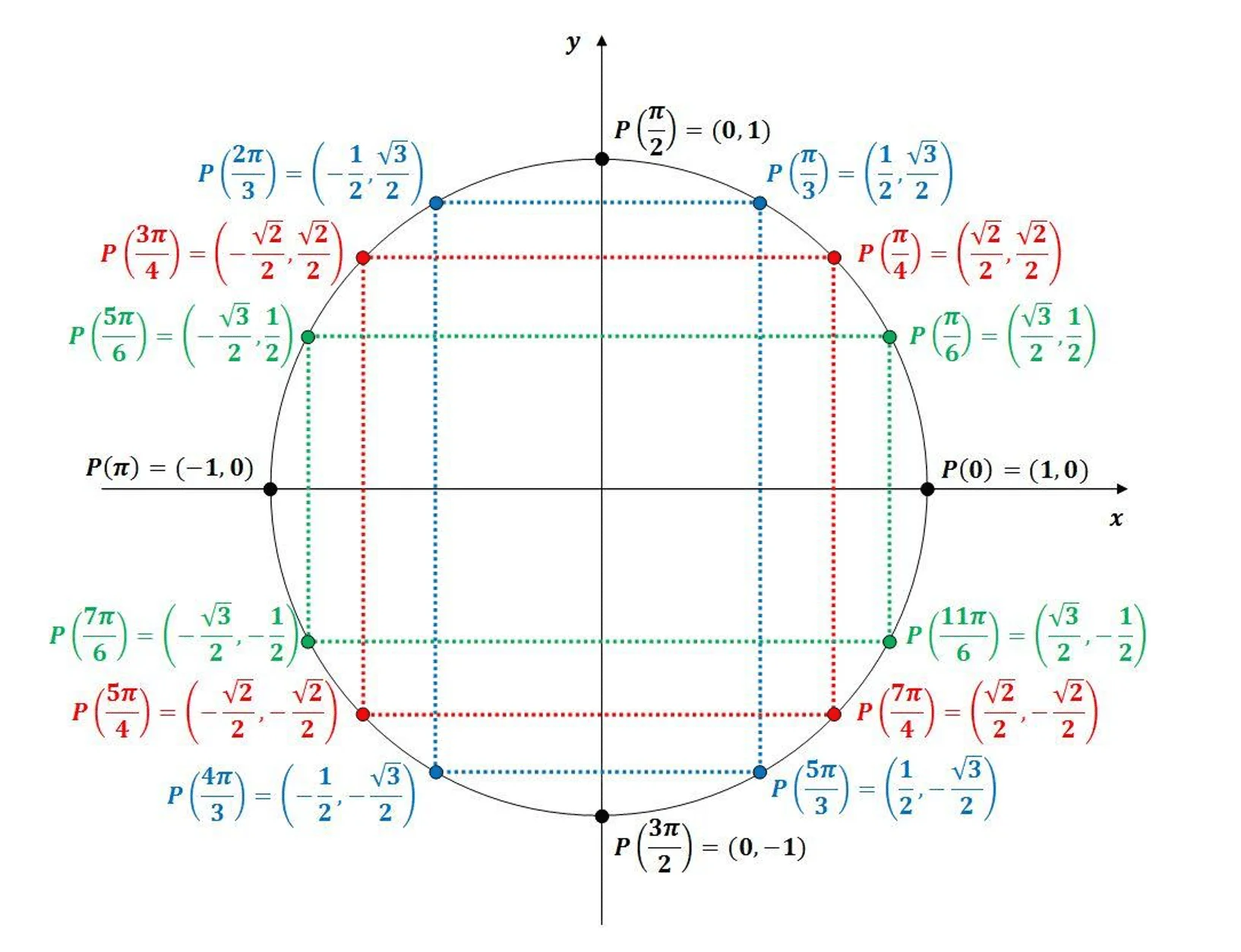
Au cours de vos études, vous avez certainement déjà vu cette espèce de cercle qui comporte des dizaines de valeurs, des milliers de points et même des axes graphiques x et y ! En effet, il s’agit du fameux cercle trigonométrique.
De quoi s’agit-il exactement ?
Il s’agit en fait d’un cercle imaginé par des mathématiciens servant à résoudre des situations mathématiques ou physiques (comme les ondes). Le centre du cercle correspond à l’origine d’un plan cartésien (0,0) et son rayon est de 1 unité. Ainsi, en reliant le centre à l’extrémité d’un axe vertical ou horizontal on obtient toujours 1 comme unité.
Comment l’interpréter et l’utiliser ?
En effet, même si nous avons appris que la trigonométrie des angles et des côtés (SOHCAHTOA) se faisait en degré, il est primordial d’utiliser une nouvelle unité pour toutes les fonctions trigonométriques, soit les radians. Ceux-ci sont aussi des angles, mais d’unité différente.
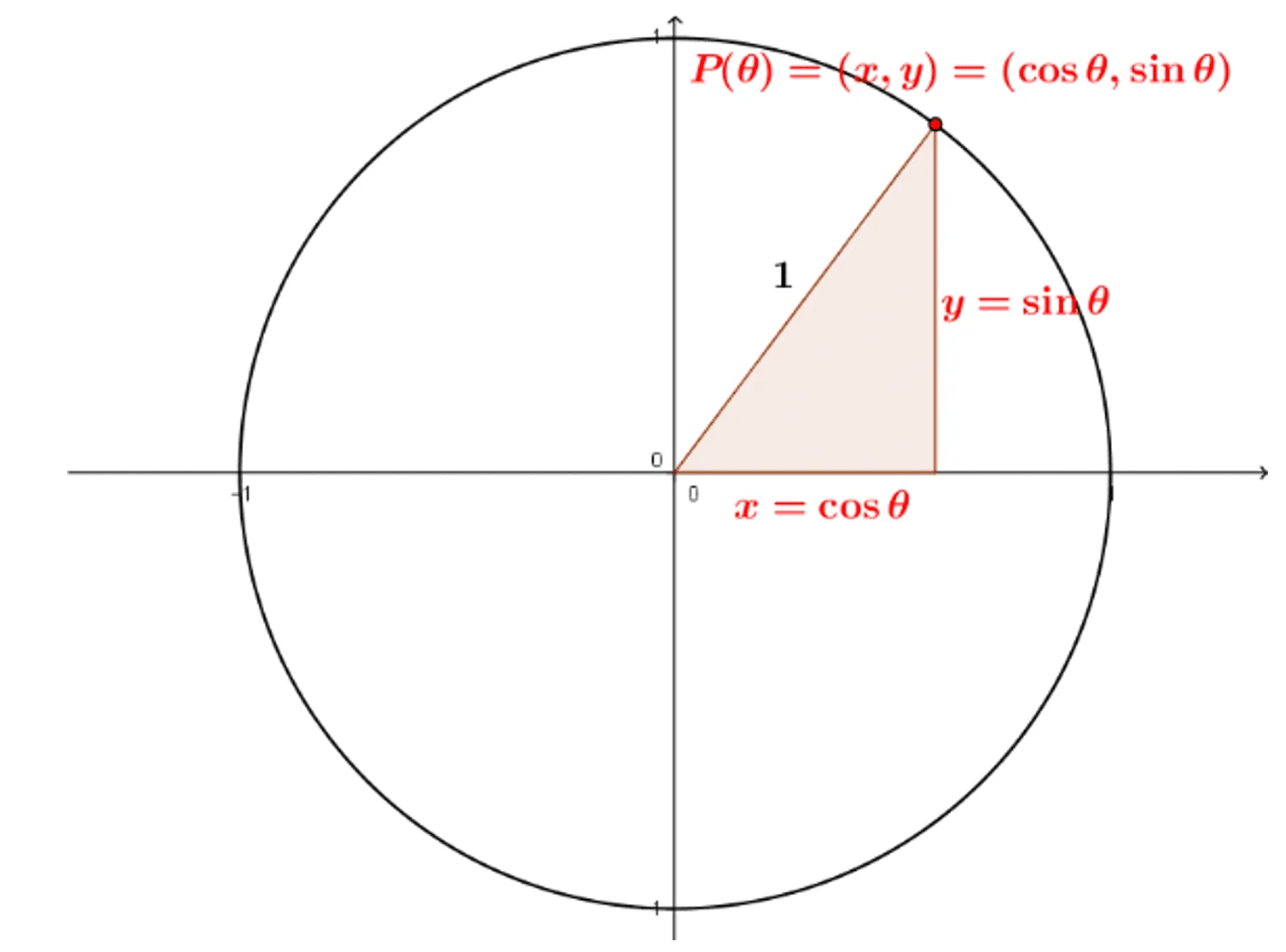
– Si on choisit un certain point du cercle, qu’on le relie au centre et que nous fermons ses extrémités pour former un triangle rectangle, nous pouvons constater les faits suivants :
- L’axe des x correspond toujours au cosinus de l’angle
- L’axe des y correspond au sinus de l’angle.
Ainsi, les coordonnées d’un point correspondent au (Cosθ, Sinθ )
Voici la conversion de degrés à radians :
2 π radians = 360 degrés. À partir de cela, il ne vous reste qu’à faire un produit croisé avec l’angle en degrés ou radians connu pour trouver celui qui est recherché.
Exemple : Convertissez un angle de 40 degrés en radians
Si 2 π radians = 360 degrés Produit croisé : ( 2 π x 40 ) / 360 = 2π/9
? radians = 40 degrés
* Prenez note d’une erreur commune chez de nombreux élèves : Ils pensent que les pi sont toujours présents. Les π ne sont pas une unité, mais bien un nombre périodique défini par ce symbole. Donc, il se peut très bien que vous tombiez sur des angles en radians sans pi. D’ailleurs, 2 π = 2 x π donc 6,283185307….. mais bon, 2π demeure plus précis.
Aussi, on peut se servir des coordonnées pour convertir des degrés en radians :
Comme nous le savons θ = Sin-1 ou Cos -1 de la valeur de Cos θ ou Sin θ .
- Dans le cercle trigo, on tourne dans le sens antihoraire en partant du point (1,0), soit à partir du rayon sur l’axe des x.
On peut aussi vérifier si un point est situé sur le cercle trigonométrique. En effet, nous pouvons visualiser un triangle rectangle avec un angle au centre, comme démontré dans le schéma précédent. Avec cela, nous pouvons utiliser le théorème de Pythagore :
x2 + y2 = rayon2. Puisque les rayons sont de longueur 1, nous pouvons conclure :
x2 + y2 = 12 , donc 1. Ainsi, pour vérifier si un point se situe sur le cercle, il suffit de remplacer les variables x et y dans l’équation. Si cela est égal à 1, le point est sur le cercle. Si ce n’est pas égal à 1, le point n’est pas sur le cercle.
Le principe de périodicité
Nous savons qu’une fonction trigonométrique est la répétition d’un segment de la fonction (d’où vient le nom période), et que des points se répètent de façon constante. Lorsque nous nous trouvons à un certain endroit sur le cercle, nous pouvons trouver une infinité d’angles complètement équivalents : en effet, il suffit de faire un tour complet (rajouter 2π ) et on se retrouve à la même position. Bien sûr, on retranche ou on ajoute 2 π selon l’intervalle dans lequel on cherche notre réponse. Par exemple, si nous avons un angle de 6 π radians et que nous avons besoin d’une réponse entre {2π, 4π}, il faudra enlever 1 ou 2 tour(s) pour se retrouver à la même position et respecter le même temps l’intervalle.
**Note : on peut rajouter ou enlever 2π autant de fois qu’il faut pour arriver à la bonne réponse.
Résolution d’équations trigonométriques
Lorsqu’il en vient résoudre des équations trigonométriques, il faut absolument utiliser le cercle trigonométrique, car il existe toujours 2 réponses possibles selon la fonction Sin (y) ou Cos (x)
D’abord, on isole de façon algébrique l’argument (toute la section entre parenthèses) et on observe si la fonction est en Sin ou Cos. Normalement, on obtient une certaine valeur de sorte à pouvoir le lire comme dans l’exemple suivant :
(0,4) = sin (x+2)
Donc, nous savons que Sin-1 (0,4) = 0,411 rad et cela vaut l’argument. Mais, on ne le touche pas directement : notre fonction est en Sin. Maintenant, nous savons que le Sin x représente l’axe des y. Sur le cercle, il y a toujours 2 points de même hauteur, donc de même valeur en y (si c’était en Cos, on fait la même chose mais pour l’axe des x, donc trouver 2 positions horizontales homologues sur le cercle).
Si nos revalidons le Sin et le Cos de l’angle :
On peut reconvertir 0,411 rad en degrés.
On obtient 23 degrés. Le Sin et le Cos de cet angle sont positifs,
donc ils se situent dans le premier quadrant.
Sur le 2e quadrant, nous retrouvons une deuxième solution qui a une position y équivalente. ATTENTION ! Les valeurs trouvées correspondent chacune à l’argument, donc x+2. N’oubliez pas de poser cette dernière égalité et de résoudre le reste de l’argument. Bien sûr, nous pouvons rajouter ou enlever 2 pi si nécessaire à chaque réponse.
Dans certains contextes, notamment ceux en sciences, il arrive qu’on doit faire un choix entre les solutions. Donc, il faut analyser le signe du cos et du sin dans chaque quadrant pour voir lequel convient le mieux à la situation. Par exemple, si nous parlons du mouvement harmonique simple (MHS) d’un ressort dont la fonction du déplacement est en Cos et qu’on donne un déplacement positif, il faudra prendre la valeur comportant un cos positif pour s’assurer que la valeur du déplacement soit positive.
Pour toutes questions ou renseignements supplémentaires, vous pouvez accéder à la capsule explicative et aux exercices de cette notion : https://youtu.be/EvZzSg0oFo4
Voici un autre article qui saura vous plaire :
Pour en savoir plus et mieux vous outiller :
Pour se pratiquer!
Par Giovanni Ménéchian
Tuteur et rédacteur
SOSprof