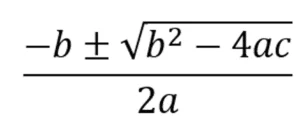Comment factoriser avec la technique somme-produit et la formule quadratique ?
*Article principalement destiné aux élèves de la 4e secondaire, 5e secondaire et aux élèves suivant les cours de mathématiques ou physique au collège.
Lorsque nous travaillons avec des expressions algébriques que nous ne pouvons pas réduire ou factoriser, il faut en venir à une autre façon de travailler avec l’expression. En effet, c’est le cas avec les expressions de la forme suivante :
Ax2 + Bx+ C.
Dans cette équation, A, B et C sont des coefficients placés devant des inconnus (les inconnus ne sont pas nécessairement x, mais peuvent prendre d’autres formes).
Généralement, nous pouvons résoudre la factorisation sous cette forme avec la méthode somme-produit. Cette méthode a pour objectif de trouver 2 nombres « m » et « n » qui permettent de trouver une équivalence à cette formule de sorte à séparer le coefficient du milieu (B) en 2 chiffres pour suivre avec une mise en évidence double. Pour se faire, il faut suivre les conditions suivantes :
- La somme des 2 nombres doit correspondre au coefficient B
- Le produit des 2 nombres doit correspondre au produit des coefficients A et C.
Ensuite, ces 2 nombres remplacent le coefficient B (tout en gardant l’inconnu, souvent x) et on effectue une mise en évidence double.
On se retrouve donc finalement avec une mise en évidence double, où il ne reste qu’à jumeler 2 groupes qui peuvent se factoriser, donnant généralement 2 parenthèses qui se multiplient. Pour trouver les nombres, la façon la plus efficace serait d’y aller par essai-erreur.
Exemple :
x2 + 7x +12
produit = a·c = 1 · 12 = 12
somme = b = 7
**Astuce : toujours commencer par chercher 2 nombres qui donnent le bon produit, ce sera moins long de trouver la bonne somme. Donc, commencez par combiner 2 nombres donnant le bon produit.
Les bons nombres sont donc 3 et 4. Pour respecter la forme de la nouvelle expression, il faudrait l’écrire selon la façon suivante :
x2 +3x + 4x +12
On peut factoriser ainsi par double mise en évidence simple :
x (x+3) + 4 (x+3)
(x+3) (x+4)
Constat : en faisant la mise en évidence double, nous pouvons constater qu’il y aura toujours la même expression entre les parenthèses, et le reste comprend la 2e parenthèse.
Utilisation de la quadratique : situation 1
Petit rappel : une fonction quadratique (parabole) possède toujours 2 abscisses qui passent par la même ordonnée (2 x passent par le même y). C’est donc pour cela qu’on retrouve le + ou – dans la formule, puisque pour la même ordonnée, il existe 2 abscisses possibles.
Il arrive souvent que la méthode somme-produit ne fonctionne pas et qu’on ne trouve pas de nombres compatibles avec la somme et le produit. Dans ce cas-là, on peut utiliser la formule quadratique pour trouver les nombres manquants.
(Note : la partie dans la racine se nomme le discriminant)
Il y a toujours 2 réponses possibles. Il suffit de remplacer les bons paramètres par les nombres qui y correspondent dans l’équation quadratique. Si on reprend l’équation d’en haut, voilà ce que cela donnerait :
– 7 + – 4 (1) (12) = -3
2 (1)
– 7- – 4 (1) (12) = -4
2 (1)
En suivant la forme de l’équation, il suffit de remplacer les paramètres :
(x- a) · (x-b)
donc (x- -3) (x- -4) = (x+3) · (x+4)
Situation 2 : absence de fatorisation
Aucun besoin de factoriser, cette formule nous permet de trouver les inconnus d’une forme quadratique. En effet, dans certains contextes, comme dans la cinématique physique, on utilise la quadratique pour résoudre un problème quand on a cette même forme de trinôme sans nécessairement avoir besoin de factoriser. Il faut correctement interpréter la situation et le contexte pour savoir quelle solution accepter ou rejeter. Par exemple, s’il s’agit de temps en secondes et qu’on obtient -8 et 4 comme réponses, on rejetterait -8 puisque le temps ne peut se compter de manière négative, et que la solution négative ne s’agirait donc que d’une solution théorique.
*Notez que pour résoudre une équation quadratique dans un contexte outre la factorisation, il faut absolument que de l’autre côté de l’équation il y ait un 0, puisque c’est une des formes de l’équation quadratique. Donc de la forme suivante :
Ax2 + Bx+ C = 0.
Voici une vidéo qui résume l’article pour aider votre compréhension :
Voici un autre article qui saura vous plaire :
Pour en savoir plus et mieux vous outiller :
Pour se pratiquer!