Comment utiliser le théorème de Pythagore?
* Article principalement destiné aux élèves de secondaire 3, 4, 5 et aux élèves des cours de mathématiques et physique collégiaux.
Nous avons tous entendu parler d’un fameux théorème impliquant des racines, des exposants et quelques lettres portant une désignation particulière, le tout au nom d’un grand mathématicien…le fameux théorème de Pythagore !
De quoi s’agit-il exactement ?
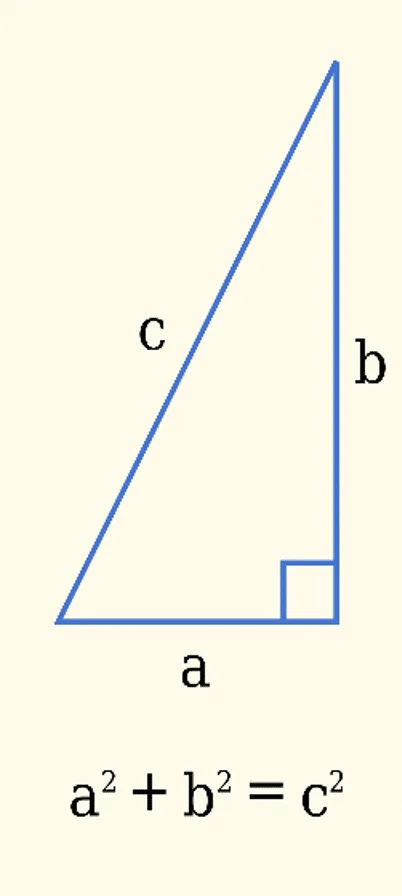
Le théorème de pythagore est en fait une relation présente entre les 3 côtés d’un triangle rectangle. Elle permet de trouver la mesure d’un des côtés manquants lorsque nous connaissons les deux autres mesures. Chaque côté d’un triangle rectangle possède un nom particulier. Les trois cotés sont les suivants :
– Cathète (a)
– Cathète (b)
– Hypoténuse (c)
* NOTE* Le théorème s’applique SEULEMENT dans un triangle rectangle. Il est donc essentiel de vérifier la présence d’un angle droit dans le triangle pour pouvoir appliquer la relation.
Les cathètes a et b sont toujours les 2 côtés adjacents à l’angle droit. Nous pouvons poser de manière aléatoire quel côté est le a et quel côté est le b (cela n’affecte pas le calcul).
L’hypoténuse est le côté le plus long du triangle rectangle. Plus simplement, c’est le côté qui est opposé à l’angle droit (le côté qui ne touche pas l’angle droit)
La relation de Pythagore se décrit comme cela :
(mesure de la cathète 1)2 + (mesure de la cathète 2)2 = (mesure de l’hypoténuse)2
a2 + b2 = c2
*Pour trouver la mesure de l’hypoténuse, il faut donc appliquer la racine de la somme du carré des cathètes. De même, en utilisant un raisonnement algébrique, nous pouvons déterminer la mesure d’une cathète manquante.
Exemple 1
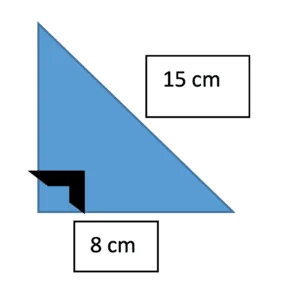
L’hypoténuse d’un triangle rectangle mesure 15 cm. Sachant qu’une des cathètes mesure 8 cm, quelle est la mesure de l’autre cathète ?
– Voici une illustration de la situation :
Tel que mentionné, il n’importe pas quel côté adjacent à l’angle droit est a ou b. Étant donné que le dessin n’est pas à l’échelle, nous aurions pu mettre le 8cm sur le côté, cela ne change rien au calcul.
a2 + b2 = c2
82 + b2 = 152
b2 = 152 – 82
b= √ 152 – 82
b = 12,68 donc 12,68 cm.
Validation de la réponse (remplacer toutes les données dans la relation et vérifier que le tout est bon et égal des 2 côtés de l’équation):
82 + 12,682 = 152
225 = 225
Bonne réponse !
Application du théorème dans d’autres contextes
Une fois que nous connaissons ce théorème, nous pouvons l’utiliser dans d’autres contextes mathématiques ou même en physique. Par exemple, lorsque nous cherchons l’aire ou le volume d’un cône ou d’un d’une pyramide et que nous ne connaissons pas la hauteur, nous pouvons nous servir de l’apothème du solide et effectuer le théorème de Pythagore pour trouver la hauteur manquante. Aussi, nous pouvons nous en servir dans les vecteurs, comme pour trouver la norme.
Voici une vidéo qui résume l’article pour aider votre compréhension :
Voici un autre article qui saura vous plaire :
Pour en savoir plus et mieux vous outiller :
Pour se pratiquer!