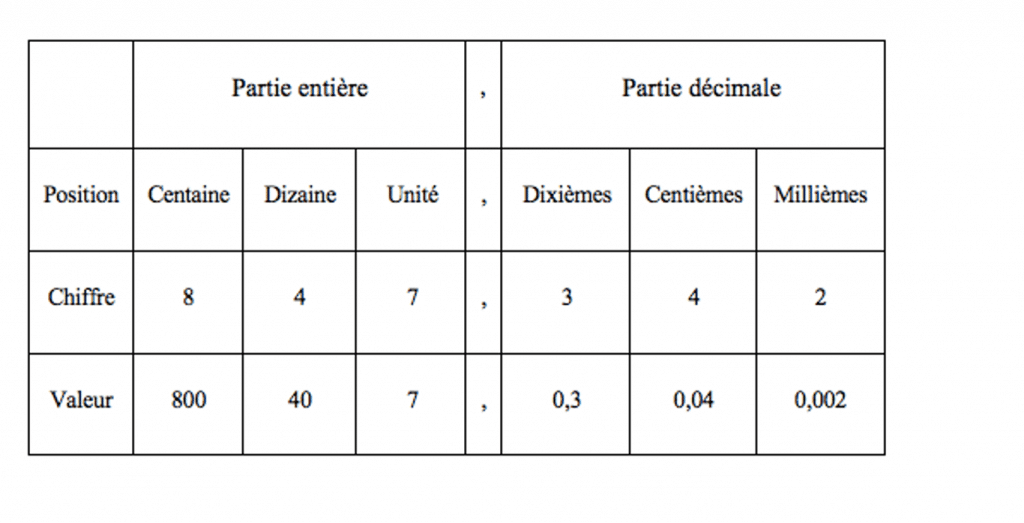
Les nombres décimaux sont formés de deux parties, une partie entière et une partie décimale. La partie entière est à gauche de la virgule tandis que la partie décimale est à droite de la virgule. La partie décimale d’un nombre correspond à la division d’une unité par 10, 100, 1000, etc.
- Lorsque l’on divise une unité par 10, on obtient des dixièmes.
- Lorsque l’on divise une unité par 100, on obtient des centièmes.
- Lorsque l’on divise une unité par 1000, on obtient des millièmes.
Dans une unité, il y a 10 dixièmes, 100 centièmes et 1000 millièmes.
Afin de bien comprendre les nombres décimaux, il est important de savoir reconnaître les positions des chiffres ainsi que la valeur de chacune des positions.
Il est important de noter qu’en français, les nombres décimaux sont écrits avec une virgule ( , ) et non avec un point ( . ) comme en anglais.
Nommer les nombres décimaux
Lorsqu’il n’y a qu’un chiffre après la virgule : prenons par exemple le nombre 847,3.
- La première étape consiste à nommer la partie des entiers.
- La deuxième étape consiste à remplacer la virgule par un (et).
- La troisième étape consiste à nommer le nombre après la virgule ainsi que la position qu’il occupe.
Le nombre 847,8 se dit donc : 847 et 3 dixièmes.
Lorsqu’il y a plusieurs chiffres après la virgule : prenons par exemple le nombre 847,342.
- La première étape consiste à nommer la partie des entiers.
- La deuxième étape consiste à remplacer la virgule par un (et).
- La troisième étape consiste à nommer la partie après la virgule ainsi que la position qu’occupe le dernier chiffre.
Le nombre 847,342 se dit donc : 847 et 342 millièmes.
Les nombres décimaux et les fractions
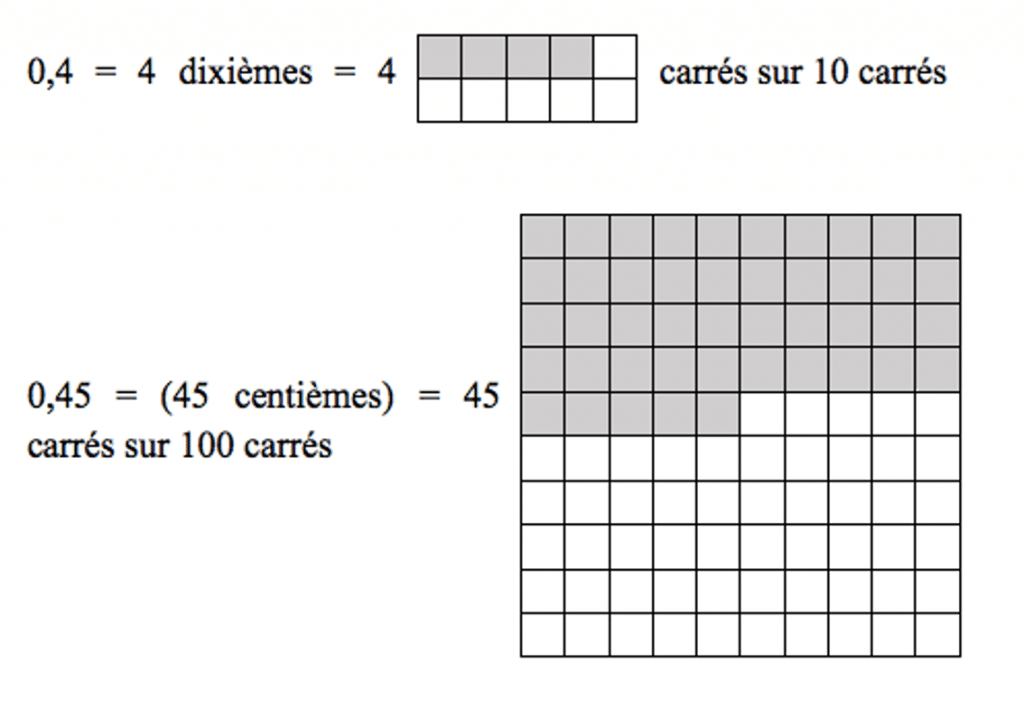
Il est important de comprendre que la partie décimale d’un nombre représente une fraction.
Décomposition d’un nombre décimal
Comme pour un nombre entier, il est possible de décomposer un nombre décimal.
1) En séparant la partie décimale de la partie entière.
Prenons par exemple le nombre 847,342.
- 847,342 = 847 + 342/1000
Prenons par exemple le nombre 57,48.
- 57,48 = 57 + 48/100
2) En utilisant la valeur de chacun des chiffres.
Prenons par exemple le nombre 847,342.
- 847,342 = (8 x 100) + (4 x 10) + (7 x 1) + (3 x 0,1) + (4 x 0,01) + (2 x 0,001)
Prenons par exemple le nombre 57,48.
- 57,48 = (5 x 10) + (7 x 1) + (4 x 0,1) + (8 x 0,01)
Pour en savoir plus et mieux vous outiller :
- Enseignez au suivant
- Allo prof : la notation décimale
Voici un autre article de la même auteure:
Auteure: Frédérique Fortier, enseignante et tutrice chez SOSprof